对线性规划的思考

前言

线性规划内容，是高中阶段体现数形结合思想最突出的数学素材；

预备知识

• 倾斜角和斜率的关系；直线的倾斜角的范围\(\theta\in [0，\pi)\)；

• 分式裂项；
• 直线的斜截式方程；
• 直线的旋转+平移；
• 点到直线的距离；

考查角度

设\(x，y\)满足约束条件\(\left\{\begin{array}{l}{x\ge 0}\\{y\ge x}\\{4x+3y\leq 12}\end{array}\right.\)，求下列代数式的值：

• 截距型：求\(z=2x-y\)的取值范围。

引申：如求\(4x^2-4xy+y^2+3=(2x-y)^2+3=z^2+3\)

• 斜率型：求\(z=\cfrac{y+2}{x-1}\)的取值范围。

引申：如求\(z=\cfrac{x-1}{y+2}\)，

引申：\(z=\cfrac{(y+2)^2}{(x-1)^2}\)，

引申：求\(z=\cfrac{2y+4}{3x-3}=\cfrac{2}{3}\times \cfrac{y+2}{x-1}\)，

引申：求\(z=\cfrac{x+2y+3}{x+1}=1+2\times \cfrac{y+1}{x+1}\)

• 距离型：求\(z=\sqrt{x^2+2x+1+y^2-4y+4}=\sqrt{(x+1)^2+(y-2)^2}\)。

引申：如求\(z=\sqrt{x^2+2x+y^2-4y}\)，

引申：\(z=x^2+2x+y^2-4y\)，

引申：\(z=\cfrac{1}{x^2+2x+y^2-4y}\)，

• 综合型：求\(|2x-y|\)的取值范围；求\(\sqrt{2x-y}\)的取值范围。
• 你试着总结过这些命题的角度吗？如：

截距+常数，截距的倍数，截距的平方；

斜率+常数，斜率的倍数，斜率的平方；

距离+常数，距离的倍数，距离的平方等等。

作图难点

• 约束条件中是线性函数

【例】\(\begin{cases} y^2-x^2 \leq0 \\ 1\leq x\leq 3\end{cases}\)先转化为\(\begin{cases} y-x \ge 0 \\ y+x \leq 0 \\ 1\leq x\leq 3\end{cases}\) 或者\(\begin{cases} y-x \leq 0 \\ y+x \ge 0 \\ 1\leq x\leq 3\end{cases}\)

• 约束条件中有非线性函数

【例】\(\begin{cases} y\ge x^2 \\ 0\leq x\leq 2 \\ 0\leq y\leq 2 \end{cases}\)

• 约束条件中有绝对值函数

【例】$|x|+|y|\leq 1 $必须转化为线性的约束条件

\(\begin{cases} x\ge 0 \\ y\ge 0 \\ x+y \leq 1 \end{cases}\)或者\(\begin{cases} x\ge 0 \\ y< 0 \\ x-y \leq 1 \end{cases}\)或者\(\begin{cases} x< 0 \\ y\ge 0 \\ -x+y \leq 1 \end{cases}\)或者\(\begin{cases} x< 0 \\ y< 0 \\ -x-y \leq 1 \end{cases}\)

• 约束条件中有参数的情形；

设\(k>1\)，在约束条件\(\begin{cases} y\ge x \\ y\leq kx \\ x+y\leq 1\end{cases}\)下，

角度例说

设不等式组\(\begin{cases}x + y \ge 3\\x - y \ge - 1\\ 2x - y \le 3\end{cases}\)表示的平面区域为D.

（1）求目标函数\(z=2x-3y\)的最值.

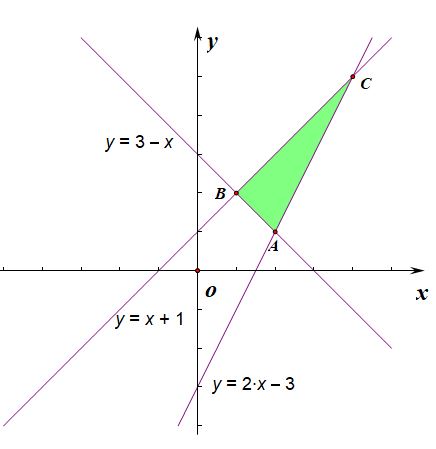
（2）求目标函数\(z=x^2+y^2-6x-4y+10\)的最值.

（3）求目标函数\(z=\cfrac{y}{x}\)的最值；目标函数\(z=\cfrac{x^2+y^2}{xy}\)的最值；

分析：\(z=\cfrac{x^2+y^2}{xy}=\cfrac{x}{y}+\cfrac{y}{x}=k+\cfrac{1}{k}\)；

（4）求目标函数\(z=\cfrac{2y-5}{x+2}\)的最值；求目标函数\(z=\cfrac{y-4}{2x-3}\)的最值；

（5）若目标函数\(z=ax+y\)取最小值时的最优解有无穷多个，求\(a\)值；

分析：难点，注意目标函数的旋转和平移；\(-a=-1\)或\(-a=2\)；

（6）若目标函数\(z=ax+y\)取最小值时的最优解仅为一个，求\(a\)的取值范围；

分析：难点，注意目标函数的旋转和平移；\((-\infty，-2)\cup(-2，1)\cup (1，+\infty)\)；

（7）若目标函数\(z=ax+y\)的最小值是\(-2\)，求\(a\)的值；

分析：难点，注意目标函数的旋转和平移；

①当\(0<-a<2\)时，即\(-2<a<0\)时，过点\(A(2，1)\)取到最小值，为\(2a+1=-2\)，解得\(a=-\cfrac{3}{2}\)，

②当\(-a>2\)时，即\(a<-2\)时，过点\(C(4，5)\)取到最小值，为\(4a+5=-2\)，解得\(a=-\cfrac{7}{4}\)，

③当\(-a<-1\)时，即\(a>1\)时，过点\(B(1，2)\)取到最小值，为\(a+2=-2\)，解得\(a=-4\)，

综上所述，\(a=-\cfrac{3}{2}\)；

（8）求函数\(|3x-4y+12|\)的取值范围。

法1：先求出\(z=3x+4y+12\)的取值范围，再求\(|3x-4y+12|\)的取值范围。

法2：\(|3x-4y+12|=5\times\cfrac{|3x-4y+12|}{\sqrt{3^2+4^2}}\)，所求即可行域中的动点\(P(x，y)\)到直线\(3x-4y+12=0\)的距离的5倍；

（9）求直线\(3x-y-1=0\)与区域\(D\)的公共点的个数。

（10）若平面区域夹在两条平行直线之间，则这两条平行直线间的最短距离为多少？

分析：平面区域夹在两条平行直线之间，通过旋转可以看出，只有平行线中的一条和某条边界重合(比如\(BC\))，另一条过边界点(比如\(A\))时距离是最小的，故转化为比较三个点线距的大小。

（11）已知\(\left\{\begin{array}{l}{x-y-1\leq 0}\\{x+y-6\leq 0}\\{x\ge 1}\end{array}\right.\)，求\(x\cdot y\) 的取值范围；\([0，9]\)

分析：从形入手分析，令\(x\cdot y=k\)，则\(y=\cfrac{k}{x}\)，图像

（12）若\(ax-y+1-a=0\)恒成立，求\(a\)的取值范围；

分析：转化为\(y=ax+1-a\)，将参数放置在斜率和截距两个位置，不利于观察总结；

或转化为\(a=\cfrac{y-1}{x-1}\)，显然后者的转化思路更利用解决问题；